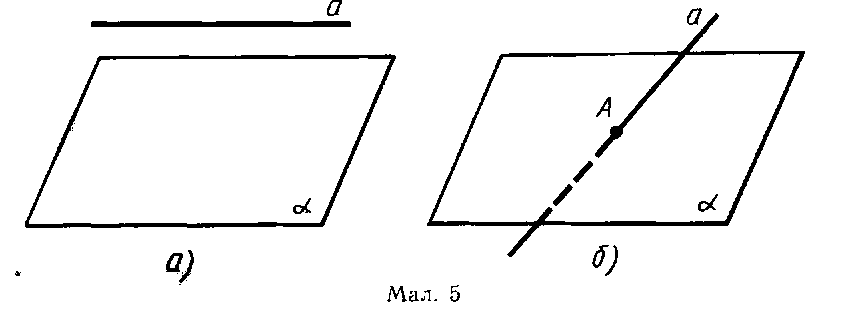
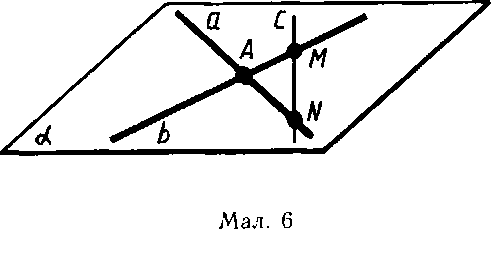
Переглянути всі підручники << < 2 3 4 5 6 7 8 9 10 11 > >>   Задача (9). Дано дві різні прямі, які перетинаються в точці А. Доведіть, що всі прямі, які перетинають обидві дані прямі й не проходять через точку А, лежать в одній площині. Розв'язання. Проведемо через дані прямі а і b площи­ну α (мал. 6). Це можна зробити за аксіомою С3. Пряма с, яка перетинає дані прямі, має з площиною α дві спільні точки М і N (точки перетину з даними прямими). За теоремою 1.2 ця пряма повинна лежати у площині α. 4. ІСНУВАННЯ ПЛОЩИНИ, ЯКА ПРОХОДИТЬ ЧЕРЕЗ ТРИ ДАНІ ТОЧКИ Теорема 1.3. Через три точки, які не лежать на одній прямій, можна провести площину і до того ж тільки одну. Доведення. Нехай А, В, С — три дані точки, які не лежать на одній прямій (мал. 7). Проведемо прямі АВ і АС; вони різні, бо точки А, В, С не лежать на одній прямій. За аксіомою С3 через пря­мі АВ і АС можна провести площину α. Ця площина містить точки А, В, С. Доведемо, що площина α, яка проходить через точки А, В, С, єдина. Справді, площина, яка проходить через точки А, В, С, за теоремою 1.2 містить прямі АВ і АС. А за аксіомою С3 така площи­на єдина.   Переглянути всі підручники << < 2 3 4 5 6 7 8 9 10 11 > >>