|
§ 8. ОБ'ЄМИ І ПОВЕРХНІ ТІЛ ОБЕРТАННЯ
73. ОБ'ЄМ ЦИЛІНДРА
Якщо тіло просте, тобто допускає розбиття на скінченну кількість трикутних пірамід, то його об'єм дорівнює сумі об'ємів цих пірамід. Для довільного тіла об'єм означають таким чином.
Дане тіло має об'єм V, якщо існують прості тіла, які містять його, і прості тіла, які містяться в ньому, з об'ємами, що як завгодно мало відрізняються від V.
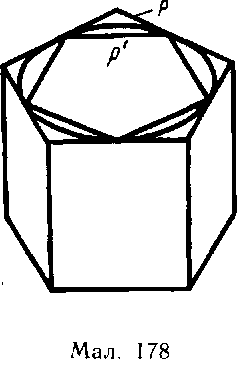
Застосуємо це означення для знаходження об'єму циліндра з радіусом основи R і висотою Н.
У процесі виведення формули для площі круга було побудовано такі два n-кутники (один, який містить круг, а другий — міститься у крузі), що їх площі при необмеженому збільшенні n необмежено наближалися до площі круга. Побудуємо такі многокутники для круга в основі циліндра. Нехай Р — многокутник, який
|
|

