|
|
|
|
|
|
|
|
|
§ 7. ОБ'ЄМИ МНОГОГРАННИКІВ
65. ПОНЯТТЯ ОБ'ЄМУ
Так само, як для фігур на площині вводиться поняття площі, для тіл у просторі вводиться поняття об'єму. Спочатку розглянемо тільки прості тіла. Тіло називається простим, якщо його можна розбити на скінченну кількість трикутних пірамід.
Для простих тіл об'єм — це додатна величина, числове значення якої має такі властивості:
1. Рівні тіла мають рівні об'єми.
2. Якщо тіло розбито на частини, які є простими тілами, то об'єм цього тіла дорівнює сумі об'ємів його частин.
3. Об'єм куба, ребро якого дорівнює одиниці довжини, дорівнює одиниці.
Якщо куб, про який ідеться в означенні, має ребро 1 см, то об'єм буде у кубічних сантиметрах; якщо ребро куба дорівнює 1 м, то — у кубічних метрах; якщо ребро куба дорівнює 1 км, то об'єм — у кубічних кілометрах і т. д.
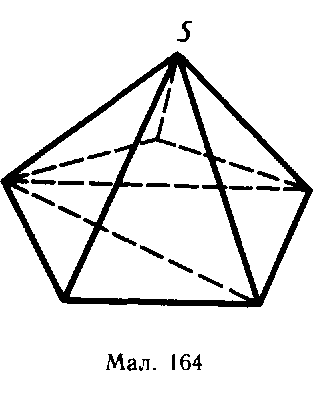
Прикладом простого тіла є довільний опуклий многогранник. Його можна розбити на скінченну кількість трикутних пірамід таким чином. Візьмемо яку-небудь вершину S многогранника. Розіб'ємо на трикутники всі грані многогранника, які не містять вершину S. Тоді трикутні піраміди, для яких основами є ці трикутники, а спільною вершиною точка S, дають розбиття многогранника на трикутні піраміди. На малюнку 164 показано таке розбиття для довільної піраміди.
|
|
|
|
|
|
66. ОБ'ЄМ ПРЯМОКУТНОГО ПАРАЛЕЛЕПІПЕДА
Знайдемо об'єм прямокутного паралелепіпеда з лінійними розмірами а, b, с. Для цього спочатку доведемо, що об'єми двох прямокутних паралелепіпедів з рівними основами відносяться, як їх висоти.
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|

