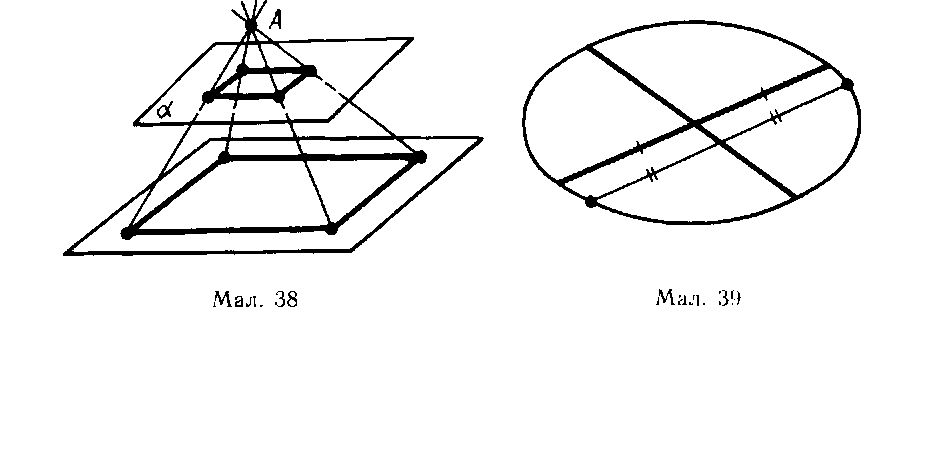
Переглянути всі підручники << < 18 19 20 21 22 23 24 25 26 27 > >>   35. Дано три паралельні площини: α1,α2,α3   . Нехай Х1, Х2, Х3— точки перетину даних площин з довільною прямою. Доведіть, що відношення довжин відрізків Х1Х2:Х2Х3 не залежить від прямої, тобто однакове для будь-яких двох прямих. 36. Дано чотири паралельні прямі. Доведіть, що коли яка-небудь площина перетинає ці прямі у вершинах паралелограма, то будь-яка площина, не паралельна даним прямим, перетинає їх у вершинах деякого паралелограма. 37. Дано паралельну проекцію трикутника. Як побудувати проек­ції медіан цього трикутника? 38. Дано паралельну проекцію трикутника. Що є проекцією серед­ньої лінії трикутника? 39. Чи може при паралельному проектуванні паралелограма ви­йти трапеція? Відповідь поясніть. 40. Чи може проекція паралелограма при паралельному проекту­ванні бути квадратом? 41. Доведіть, що паралельна проекція центрально-симетричної фі­гури теж є центрально-симетричною фігурою. 42. Дано паралельну проекцію кола і його діаметра (мал. 39). Як побудувати проекцію перпендикулярного діаметра? § 3. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ І ПЛОЩИН 14. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ У ПРОСТОРІ Як і на площині, дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 3.1. Якщо дві прямі, які перетинаються, паралельні відповідно двом перпендикулярним прямим, то вони теж перпенди­кулярні.   Переглянути всі підручники << < 18 19 20 21 22 23 24 25 26 27 > >>