| |
Поверхня призми складається з основ і бічної поверхні. Бічна поверхня складається з паралелограмів. Кожен з цих паралелограмів має дві сторони, які є відповідними сторонами основи, а дві інші — суміжними бічними ребрами.
Висотою призми називається відстань між площинами її основ. Відрізок, який сполучає дві вершини призми, що не належать одній грані, називається діагоналлю призми.
Призма називається n-кутною, якщо її основи n-кутники. Надалі ми розглядатимемо тільки призми, у яких основи — опуклі многокутники. Такі призми є опуклими многогранниками. На малюнку 95 зображено п'ятикутну призму. Основами її є п'ятикутники А1А2...А5, А'1А'2...А'5. XX'— відрізок, який сполучає відповідні точки основ. Бічні ребра призми — відрізки А1А'1, А2А'2, ... , А5А'5. Бічні грані призми — паралелограми А1А2А'2А'1, А2А3А'3А'2, ... .
41. ЗОБРАЖЕННЯ ПРИЗМИ І ПОБУДОВА ЇЇ ПЕРЕРІЗІВ
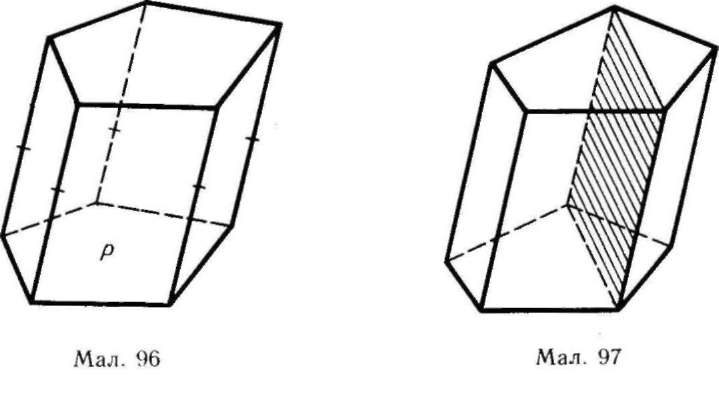
Відповідно до правил паралельного проектування призму зображають таким чином. Спочатку будують одну з основ Р (мал. 96). Це деякий плоский многокутник. Потім з вершин многокутника Р проводять бічні ребра призми у вигляді паралельних відрізків однакової довжини. Кінці цих відрізків сполучають і дістають другу основу призми. Невидимі ребра зображають штриховими лініями.
Перерізи призми площинами, паралельними бічним ребрам, є паралелограмами. Зокрема, паралелограмами є діагональні перерізи. Це перерізи призми площинами, що проходять через два бічні ребра, які не належать одній грані (мал. 97).
На практиці, зокрема, у процесі розв'язування задач часто доводиться будувати переріз призми площиною, що проходить через задану пряму, яка лежить у площині однієї з основ призми.
|
|