|
|
|
|
|
|
|
|
|
Якщо дана точка А належить бічній грані, то перетин цієї грані з січною площиною будують, як показано на малюнку 98, б. А саме, спочатку будують точку D, в якій площина грані перетинає даний слід g. Потім проводять пряму через точки А і D). Відрізок ВС прямої АD на грані, що розглядається, і є перетином цієї грані з січною площиною. Якщо грань, яка містить точку А, паралельна сліду g, то січна площина перетинає цю грань по відрізку ВС, що проходить через точку А і паралельний прямій g.
Кінці відрізка ВС належать і сусіднім граням. Тому таким способом можна побудувати перетин цих граней з нашою січною площиною. І так далі.
На малюнку 99 показано побудову перерізу чотирикутної призми площиною, яка проходить через пряму а площини нижньої основи призми і точку А, яка лежить на одному з бічних ребер.
|
|
|
|
|
|
42. ПРЯМА ПРИЗМА
|
|
|
|
|
|
Призма називається прямою, якщо її бічні ребра перпендикулярні до основ. У противному разі призма називається похилою.
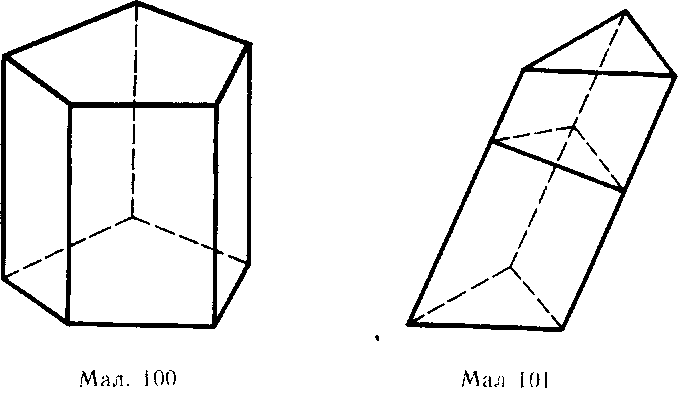
Бічні грані прямої призми - прямокутники. Зображаючи пряму призму на малюнку, бічні ребра звичайно проводять вертикально (мал. 100).
Пряма призма називається правильною, якщо її основи є правильними многокутниками.
Бічною поверхнею (точніше, площею бічної поверхні) призми називається сума площ бічних граней. Повна поверхня призми дорівнює сумі бічної поверхні і площ основ.
Теорема 5.1. Бічна поверхня прямої призми дорівнює добутку периметра основи на висоту призми, тобто на довжину бічного ребра.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
