|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
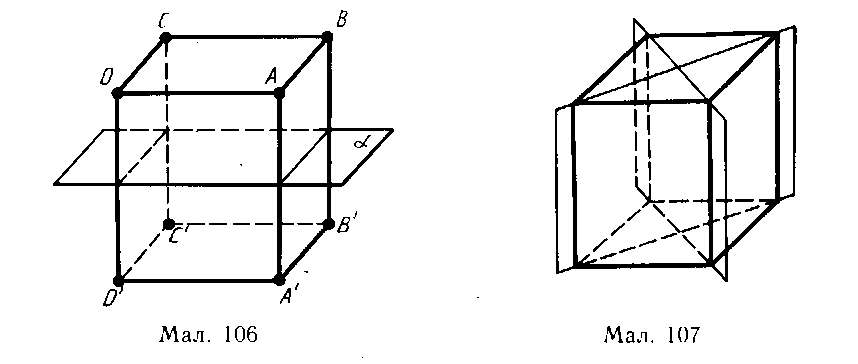
Якщо ж у паралелепіпеда два лінійних розміри однакові, то він має ще дві площини симетрії. Це площини діагональних перерізів, показані на малюнку 107.
Якщо у паралелепіпеда всі лінійні розміри однакові, тобто він є кубом, то площина будь-якого його діагонального перерізу є площиною симетрії. Таким чином, куб має дев'ять площин симетрії.
|
|
| |
|
|
| |
47. ПІРАМІДА
Пірамідою називається многогранник, який складається з плоского многокутника — основи піраміди, точки, яка не лежить у площині основи,— вершини піраміди і всіх відрізків, що сполучають вершину піраміди з точками основи (мал. 108).
Відрізки, що сполучають вершину піраміди з вершинами основи, називаються бічними ребрами.
Поверхня піраміди складається з основи і бічних граней. Кожна бічна грань — трикутник. Однією з його вершин є вершина піраміди, а протилежною стороною — сторона основи піраміди.
Висотою піраміди називається перпендикуляр, опущений з вершини піраміди на площину основи.
Піраміда називається n-кутною, якщо її основою є n-кутник. Трикутна піраміда називається також тетраедром.
|
|
| |
|
|
| |

|
|
| |
|
|
| |
|
|
|

