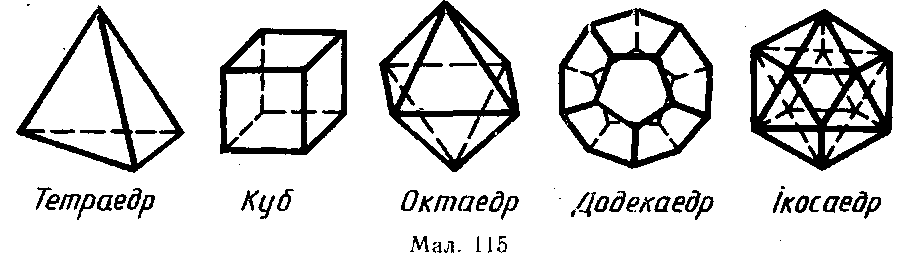|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
51. ПРАВИЛЬНІ МНОГОГРАННИКИ
Опуклий многогранник називається правильним, якщо його грані є правильними многокутниками з однією й тією самою кількістю сторін, а в кожній вершині многогранника сходиться одне й те ж число ребер.
Існує п'ять типів правильних опуклих многогранників (мал. 115): правильний тетраедр, куб, октаедр, додекаедр, ікосаедр.
|
|
|
|
|
|
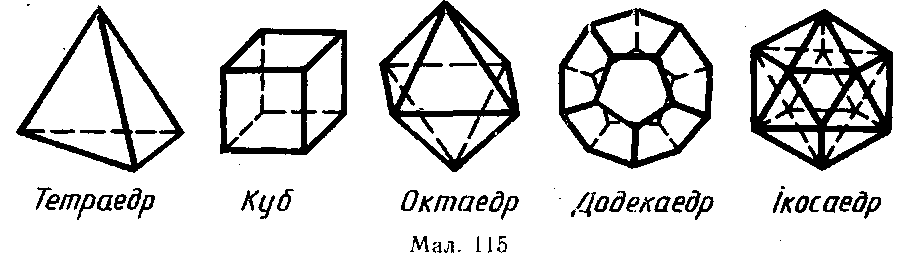
|
|
|
|
|
|
У правильного тетраедра грані — правильні трикутники; у кожній вершині сходиться по три ребра. Тетраедр — трикутна піраміда, всі ребра якої рівні.
У куба всі грані — квадрати; у кожній вершині сходиться по три ребра. Куб — прямокутний паралелепіпед з однаковими ребрами.
У октаедра грані — правильні трикутники, але на відміну від тетраедра у кожній його вершині сходиться по чотири ребра.
У додекаедра грані — правильні п'ятикутники. У кожній вершині його сходиться по три ребра.
У ікосаедра грані — правильні трикутники, але на відміну від тетраедра і октаедра у кожній вершині сходиться по п'ять ребер.
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|