|
5. Доведіть, що переріз призми, паралельний основам, дорівнює основам.
6. Скільки діагоналей має n-кутна призма?
7. Побудуйте переріз чотирикутної призми площиною, яка проходить через сторону основи і одну з вершин другої основи.
8. Побудуйте переріз чотирикутної призми площиною, яка проходить через три точки на бічних ребрах призми.
9. Одне бічне ребро призми перпендикулярне до площини основи. Доведіть, що решта бічних ребер теж перпендикулярна до площини основи.
10. У прямій трикутній призмі сторони основи дорівнюють 10 см, 17 см і 21 см, а висота призми 18 см. Знайдіть площу перерізу, проведеного через бічне ребро і меншу висоту основи.
11. Бічне ребро похилої призми дорівнює 15 см і нахилене до площини основи під кутом 30°. Знайдіть висоту призми.
12.* У похилій трикутній призмі відстань між бічними ребрами дорівнює 37 см, 13 см і 40 см. Знайдіть відстань між більшою бічною гранню і протилежним бічним ребром призми.
13. Основою призми є правильний шестикутник із стороною а, а бічні грані — квадрати. Знайдіть діагоналі призми і площі її діагональних перерізів.
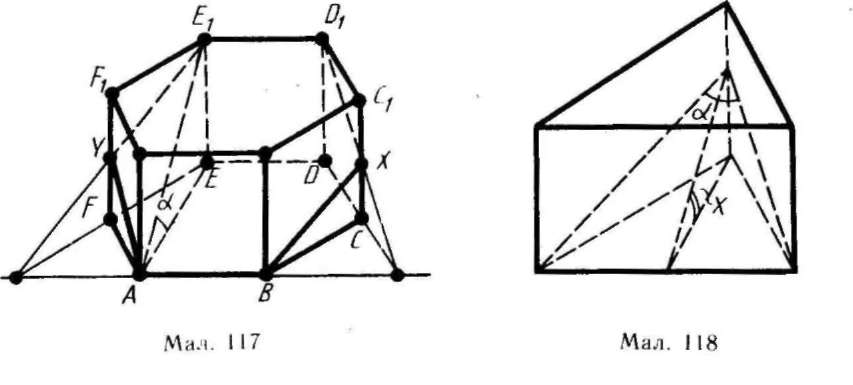
14.* У правильній шестикутній призмі, бічні грані якої — квадрати, проведіть площину через сторону нижньої основи і протилежну їй сторону верхньої основи. Сторона основи дорівнює а. Знайдіть площу побудованого перерізу (мал. 117).
15. Через сторону нижньої основи правильної трикутної призми проведено площину, яка перетинає бічні грані по відрізках, що утворюють кут а. Знайдіть кут нахилу цієї площини до основи призми (мал. 118).
|
|